ATRAVÉS DO UNIVERSO: A floresta e o cosmos

O GEDAI publica o trigésimo sexto artigo da série ATRAVÉS DO UNIVERSO, coluna mensal do prof. Domingos Soares (Departamento de Física / UFMG). Conheça mais sobre o autor em sua página eletrônica.
A floresta e o cosmos
14 de outubro de 2021
A floresta é muito utilizada na discussão da questão da escuridão do céu noturno, conhecida como “paradoxo de Olbers”. As árvores representam estrelas ou galáxias e a floresta é o universo ou um aglomerado de estrelas. Uma floresta encoberta representa o sistema, de estrelas ou de galáxias, encoberto de luz para o observador em seu interior. As condições para a floresta encoberta são semelhantes às condições para os sistemas cósmicos encobertos.
A figura 1 mostra uma floresta de eucaliptos na qual a densidade de árvores e a grossura dos troncos não é suficiente para que a mesma seja encoberta, em outras palavras, para que a visão na direção de visada seja bloqueada por um “muro” de árvores. A grandeza fundamental para a análise do encobrimento é o chamado “limite de fundo” LF. Se a dimensão da floresta na direção da linha de visada for maior do que LF, então a visão será encoberta pelo mencionado muro de troncos.

Floresta de eucaliptos de uma agroindústria que fotografei ao longo da estrada que liga Pitangui a Martinho Campos na região centro-oeste de Minas Gerais. Na direção da visada o limite de fundo não foi atingido.
O limite de fundo bidimensional
O limite de fundo é o tamanho mínimo de uma floresta para que ela se apresente encoberta a um observador. Como veremos a seguir este limite de fundo é dado pelo chamado “livre caminho médio” na floresta. Se alguém atirar, por exemplo, 50 flechas no interior de uma floresta encoberta, a distância média percorrida pela flecha até atingir um tronco é o livre caminho médio nesta floresta. Esta grandeza é muito útil em outros contextos em física, especialmente no estudo da teoria cinética dos gases e de modo geral na mecânica estatística.
Considere a “floresta” mostrada na figura 2. A floresta é vista de cima e cada ponto representa o tronco de uma árvore. Suponha que à altura dos olhos todos os troncos apresentam a largura l e cada árvore ocupa uma área igual à área total da floresta dividida pelo número de árvores lá existentes. Se o número de árvores na área circular de raio L vale N, então a área média ocupada por uma árvore será A = πL2/N. Note que a densidade de árvores na floresta — o número de árvores por unidade de área — pode ser calculado como n = N/πL2, portanto, n = 1/A.
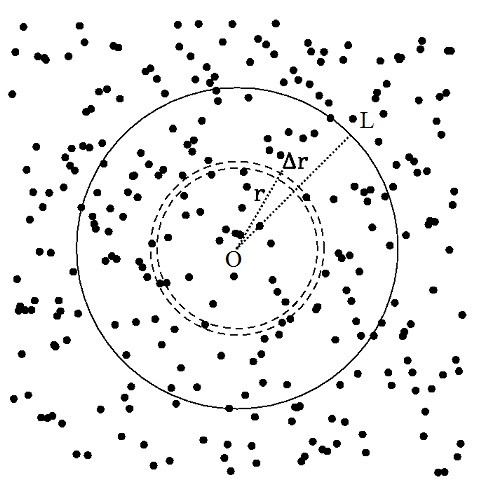
Árvores, representadas pelos pontos, distribuídas aleatoriamente numa floresta. A distância L delimita uma região da floresta que o observador em O vê recobrimento parcial de troncos.
A área recoberta dentro do anel de largura Δr mostrado na figura 2 será dada pelo número de troncos dentro do anel (n2πrΔr) multiplicado pela largura dos troncos l:
ΔArecob = n2πrΔrl.
A fração recoberta do anel, que possui comprimento 2πr, será
Δf = ΔArecob/2πr = nΔrl.
A fração recoberta até a distância L é obtida somando-se as contribuições de todos os Δr de O até L:
f = nLl = L/λ,
onde λ = 1/nl é o livre caminho médio na floresta, mencionado acima.
Ora, o recobrimento total da floresta observado a partir de O ocorrerá para a fração f = 100%, ou seja,
f = 1 =
LF/λ,
LF = λ,
onde LF é a distância L para qual f = 100%.
Substituindo a densidade de árvores n por 1/A obtemos a expressão final para o “limite de fundo” ou “distância de recobrimento” LF:
LF = A/l.
Floresta de brinquedo
A figura 3 apresenta uma “floresta de brinquedo” retangular. Ela pode ser utilizada para a verificação experimental do limite de fundo LF.
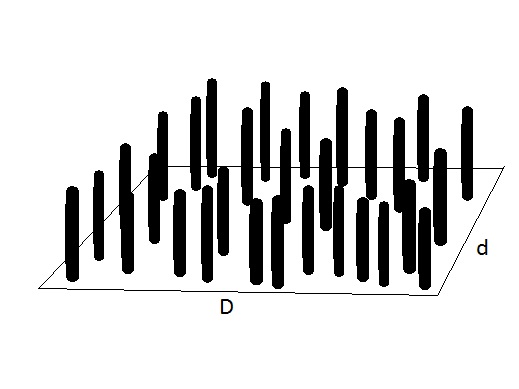
Floresta de brinquedo retangular. Os bastões representam troncos de árvores.
Existem N troncos na floresta. O valor de N não pode ser muito pequeno, de forma a garantir a validade das expressões médias utilizadas no cálculo de LF. É sempre bom lembrar que, grosso modo, a representatividade estatística de uma amostra com N elementos aumenta com N1/2 [lembrar que o desvio padrão de uma grandeza é ∝ 1/(N-1)1/2].
Os troncos podem ser confeccionados serrando-se cabos de vassoura descartados e o “terreno” da floresta pode ser uma placa de papelão duro ou de madeira, sobre o qual os troncos serão colados segundo uma distribuição aleatória.
Este é o experimento: distribuir os troncos na área total Dd. Calcular A = Dd/N, e medir l no tronco. Sugere-se medir a circunferência do tronco, em caso de troncos cilíndricos, e calcular l = circunferência/π. Calcular LF = A/l. O limite de fundo deve ser tal que seja d < LF < D. A floresta será encoberta segundo a linha de visada ao longo de D, mas não ao longo de d. Ajuste N, D e d para que isto ocorra.
As florestas de brinquedo devem servir de motivação também para as medições de campo. Escolhe-se um bosque, uma mata, mesmo uma floresta, e mede-se A — através da contagem de árvores numa área pré-estabelecida — e mede-se l médio, medindo-se a circunferência de cada tronco nesta mesma área. O valor do limite de fundo LF pode ser confrontado com a situação real. Se a mata for encoberta, LF será menor que a sua dimensão na direção da linha de visada.
Conclusão
A realização do experimento da floresta encoberta e a discussão conceitual do fenômeno é uma excelente motivação para se abordar uma das mais simples e importantes observações cosmológicas, qual seja, a escuridão do céu noturno. Esta observação inevitavelmente nos força a refletir sobre universo em que vivemos. Ela é, como vimos, referida como o paradoxo de Olbers. O paradoxo é colocado da seguinte maneira: num universo infinitamente grande e velho, ao olharmos para um ponto qualquer do céu noturno, a nossa linha de visada eventualmente deveria encontrar uma fonte de luz — uma estrela, uma galáxia — e o céu noturno deveria se nos afigurar resplandecente como a superfície do Sol. Não é assim, como todos sabemos.
O fato é que há dois pontos fundamentais e uma constatação inevitável, os quais impedem que o céu noturno seja brilhantemente insuportável. Os dois pontos:
- As fontes de luz não duram para sempre.
- A velocidade da luz é finita.
E a constatação inevitável: não há energia suficiente, em todo o universo, para que o céu noturno seja mais brilhante do que ele já é.
Curiosamente, o paradoxo de Olbers não é um paradoxo nem é de Olbers. O inglês William Thomson (1824-1907) — o lorde Kelvin —, um dos mais sagazes estudiosos da questão da escuridão do céu, afirmou em 1887, num discurso acadêmico, que em ciência não existem paradoxos; para ele, os paradoxos eram resultados de mal-entendidos, em outras palavras, do uso equivocado do conhecimento científico, dos fatos experimentais e das evidências observacionais exibidas pela Natureza. E a tal questão já era discutida muito antes de o médico e astrônomo alemão Heinrich Olbers (1758-1840) ter chamado a atenção para ela em 1823. O grande astrônomo alemão Johannes Kepler (1571-1630) foi provavelmente o primeiro a propor este problema.
A escuridão do céu deve ser bem contextualizada, para evitarmos erros. Se considerarmos outros comprimentos de onda da luz, fora da faixa visível, o céu poderá não ser escuro. Por exemplo, na faixa de micro-ondas há um brilho uniforme em todo o céu, conhecido como “Radiação de Fundo de Micro-ondas” (RFM). Este brilho uniforme de micro-ondas pode ser trivialmente observado: de acordo com um dos descobridores da RFM — o físico Robert Wilson —, 10% do “chiado” que aparece numa tela de TV, ligada a uma antena, fora de sintonia, é devido à RFM; ver seu depoimento no vídeo The Cosmology Quest, parte 2, a partir do minuto 33:00.
Um pouco mais:
==================
Domingos
Soares
FLORESTA
COSMOS
==================
